| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 배낭 문제
- 클래스
- 정처기 필기
- 문자열
- 파이썬
- 모듈러 연산 분배법칙
- 냅색 알고리즘
- 그래프 이론
- npm start
- Docker 원리
- 최장공통부분문자열
- 구현
- lazy evaluation
- dfs
- 최장공통부분수열
- 너비 우선 탐색
- 그래프탐색
- 나는 바보야...
- Python
- bfs
- LCS 알고리즘
- 다이나믹 프로그래밍
- error:0308010C:digital envelope routines::unsupported
- 일단 시도
- db replication
- 그래프 탐색
- 깊이 우선 탐색
- 수학
- Container vs VM
- 동적 계획법
- Today
- Total
Save my data
백준 1260 : DFS와 BFS (파이썬) 본문
깊이 우선 탐색과 너비 우선 탐색 기초문제이다.
- 깊이 우선 탐색 - Depth First Search
- 트리나 그래프에서 임의의 분기를 마주칠 때 마다 어떤 노드에 어떤 형태의 분기가 있다는 것을 기억만 해 놓고 계속 내려간다. 그러다가 막다른 곳(자식 노드가 없는 노드 == 리프 노드) 을 마주하게 되면 전에 기록해놓았던 분기로 되돌아가서 그 분기부터 다시 파고들어가는 것을 그 그래프의 모든 노드를 방문할 때 까지 계속 반복한다.
- 말 그대로 깊이를 우선해서 탐색하는 방법이다.
- 너비 우선 탐색 - Breadth First Search
- 트리나 그래프에서 임의의 분기를 마주치면 분기 하위의 자식 노드들을 너비 방향으로 방문해간다.
- 어떤 분기에서 그 분기의 뿌리가 되는 부모 노드의 형제 노드들을 우선적으로 방문하고 방문 순서를 기억한다. 모두 방문한 다음, 첫 번째 방문했던 형제 노드를 부모로 가지는 그 하위 형제 노드들을 방문하고 밑으로 내려가는 것이 아니라 다시 부모 노드로 되돌아와서 이번에는 두 번째 방문했던 형제를 부모로 하는 형제 노드들을 방문한다. 그런 식으로 옆으로 퍼지면서 노드의 끝까지 탐색하게 된다.
깊이 우선 탐색과 너비 우선 탐색은 모두 재귀함수로 구현할 수 있고 큐나 스택을 활용해서 구현할 수도 있다. 깊이 우선 탐색의 경우 스택과 재귀함수로 모두 구현해봤지만 개인적으로는 재귀로 구현하는 것이 더 직관적인 것 같아서 그렇게 했다. 너비 우선 탐색의 경우는 반복문을 써서 큐로 구현하는 것이 더 편했다.
그래프 초기화를 위한 코드와 dfs / bfs 구현 코드를 분리해서 살펴보자.
import sys
from collections import deque
N, M, V = [*map(int, sys.stdin.readline().split())]
graph = [[] for _ in range(N + 1)]
for _ in range(M):
i, j = map(int, sys.stdin.readline().split())
graph[i].append(j)
graph[j].append(i)
visited_dfs = []
visited_bfs = []
for edge in graph:
edge.sort()
queue = deque([])
- 먼저 N 개의 정점을 담을 노드를 만들어준다. DP 와 마찬가지로 0 번째 노드는 사용하지 않을 것이기 때문에 N + 1 개 만큼의 노드를 만든다.
- M 개의 간선을 받을 때 무방향 그래프이므로 양 노드에 서로의 노드 번호를 추가한다.
- 방문했던 번호를 기억할 visited 리스트를 만들어준다.
- bfs 에서 사용될 queue 하나를 만들어준다. (이 문제에서 dfs 쪽 queue 는 없어도 된다)
- 낮은 정점부터 볼 것이기 때문에 정렬을 한 번 해준다.
이제 dfs 코드를 살펴보자.
def dfs(v):
if v not in visited_dfs:
visited_dfs.append(v)
for i in graph[v]:
dfs(i)- 어떤 정점 v 가 들어오면
- 만약 v 가 이전에 방문되지 않았다면 새로 방문처리를 해 주고
- 해당 정점과 이어져 있는 다른 정점들 i 에 대해
- dfs 를 재귀적으로 실행한다.
백준의 두 번째 예시 입력을 따르는 경우,
처음 탐색할 정점은 3 이고 그 정점의 인접 정점은 1 과 4 이다.
그 중 첫 번째로 탐색할 인접 정점은 1 => 정점 1 에 대해 방문 처리한다.
정점 1 의 인접 정점 i (이 경우 2 와 3) 에 대해 다시 dfs 가 호출된다.
먼저 호출되는 것이 dfs(2) 이다.
만약 더 이상 탐색할 인접 정점이 없다면, (나머지 정점들이 방문 처리가 되어 실행할 명령이 없다면)
갱신된 방문 리스트만 반환한 후 함수는 실행 종료가 되고 실행 종료 후 복귀할 위치는 이전 for 문의 마지막 줄이기 때문에,
복귀 후 for 문의 다음 i 번 정점을 탐색한다. 즉, 기존에 탐색하지 않았던 분기까지 거슬러 올라가 다음 dfs 함수를 호출하며 진행된다.
이러한 진행 방식이 깊이 방향 우선으로 탐색하는 dfs 이다.
이제 bfs 코드를 살펴보자.
def bfs(v):
if v not in visited_bfs:
visited_bfs.append(v)
queue.extend(graph[v])
while queue:
i = queue.popleft()
bfs(i)- 어떤 정점 v 가 들어오면
- 만약 v 가 이전에 방문되지 않았다면 새로 방문처리를 해 주고
- queue 에 v 와 인접한 정점을 담는다.
- queue 가 비어있지 않은 동안 기존 queue 에 들어온 순서대로 bfs 를 실행한다.
queue 를 사용하는 이유는 탐색할 정점들의 순서를 정해주기 위해서이다.
어떤 정점의 인접 정점들을 extend 로 한꺼번에 넣은 다음 앞에서부터 하나씩 빼서 탐색한다.
그렇게 탐색한 어떤 정점의 인접 정점들을 queue 의 뒤에 집어넣는것은 곧 방문할 순서를 정해주는 것과 같다.
말로 풀어서 생각하면 어려운데, 트리 구조를 생각하면 쉽다.
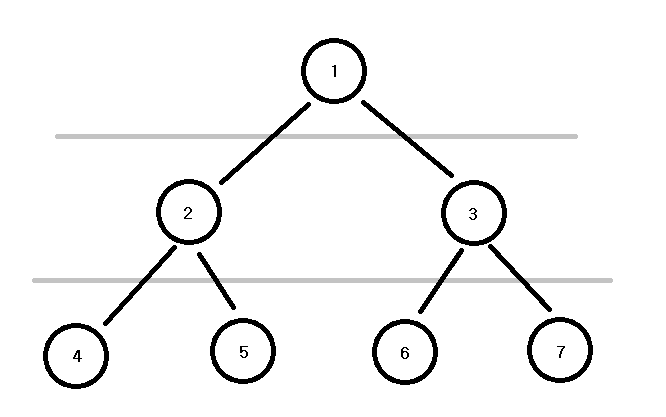
위의 그림과 같이
트리의 1층에는 근노드 1이 있고, 2층에는 2와 3, 3층에는 4와 5, 6과 7 이 있다고 했을 때,
각 층에 있는 노드를 통으로 queue 에 집어넣고 왼쪽부터 꺼내면서 탐색하는 구조이다.
선입선출 구조이므로 들어가는 순서는 (1), (2, 3), (4, 5), (6, 7) 순서일 것이고 맨 처음에 들어간 1이 가장 먼저 탐색된다.
다음 탐색 때 깊이 방향으로 탐색 될 노드들이 나 다음으로 탐색될 형제 노드의 뒤로 누적되면서 들어가기 때문에 너비 방향의 탐색이 된다.
다만 위에 써 놓은 코드는 함수를 재귀적으로 재방문하는 횟수가 많아 그냥 제출할 시 백준에서 RecursionError 가 나온다.
저 코드 그대로 쓰려면 sys 모듈의 setrecursionlimit 함수로 재귀 깊이 제한을 늘려주어야 한다.
그런 문제들을 방지하기 위해 보통의 경우 bfs 를 구현할 때는 재귀로 구현하지 않고 아래와 같이 반복문으로 구현한다고 한다.
def bfs(v):
visited_bfs.append(v)
queue.append(v)
while queue:
i = queue.popleft()
for j in graph[i]:
if j not in visited_bfs:
visited_bfs.append(j)
queue.append(j)
정리된 전체 코드는 다음과 같다.
import sys
from collections import deque
N, M, V = [*map(int, sys.stdin.readline().split())]
graph = [[] for _ in range(N + 1)]
for _ in range(M):
i, j = map(int, sys.stdin.readline().split())
graph[i].append(j)
graph[j].append(i)
visited_dfs = []
visited_bfs = []
for edge in graph:
edge.sort()
queue = deque([])
def dfs(v):
if v not in visited_dfs:
visited_dfs.append(v)
for i in graph[v]:
dfs(i)
def bfs(v):
visited_bfs.append(v)
queue.append(v)
while queue:
i = queue.popleft()
for j in graph[i]:
if j not in visited_bfs:
visited_bfs.append(j)
queue.append(j)
dfs(V)
bfs(V)
print(*visited_dfs)
print(*visited_bfs)
재귀적으로 구현하는 경우가 있을지도 모르니 sys.setrecursionlimit() 은 잊지말고 알아두어야겠다.
'알고리즘 & SQL > 백준' 카테고리의 다른 글
| 백준 2667 : 단지번호붙이기 (0) | 2023.03.03 |
|---|---|
| 백준 2178 : 미로 탐색 (파이썬) (0) | 2023.03.02 |
| 백준 2293 : 동전 1 (0) | 2023.03.01 |
| 백준 10812 : 바구니 순서 바꾸기 (파이썬) (0) | 2023.02.27 |
| 백준 9465 : 스티커 (파이썬) (1) | 2023.02.27 |
